-
[BOJ - JAVA] 15649 - N과 M 1(백트래킹) 본문
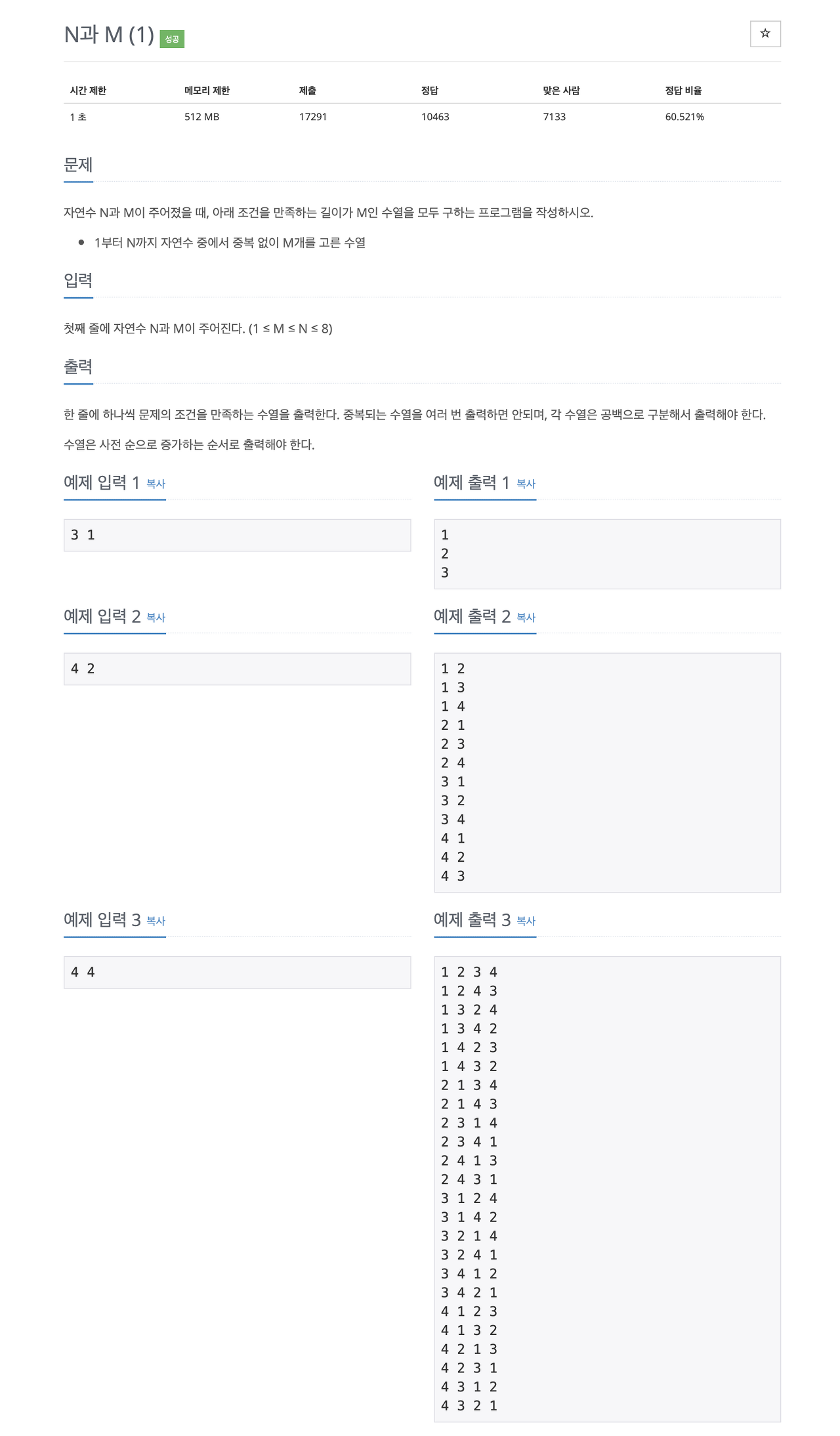
- 문제 해석
알고리즘 기법 중에는 백트래킹(Back-Tracking)이라는 기법이 있다.
되추적이라는 의미로서 어떤 노드의 유망성을 판단한 뒤 해낭 노드가 유망하지 않을 경우 부모 노드로 돌아가 다른 자식 노드를 찾는 알고리즘의 기법이다. 즉 모든 경우의 수를 찾는다는 점에서 BFS와 비슷하지만 그 중에서도 가능성이 있는 노드의 경우의 수만 찾는 기법이라고 할 수 있다.
나도 아직 공부하는 입장이라 백트래킹, 브루트포스 깊이우선탐색(DFS)의 정확한 차이를 쉽게 구분하기 어려워 여러 사이트의 정보를 인용하여 블로그를 작성하였다. 만약 지나가다 들렀으면 잘 이해하고 넘어가길 바란다.
예를 들어 "a + b + c + d = 10"을 만족하는 모든 경우의 수를 구하시오
(단, a,b,c,d는 0이 아닌 정수)
우리는 이것을 수학적 기법을 도입하여 구할 수도 있다.
확률과 통계라는 과목에는 이 a + b + c + d를 합하여 10이 되게 하는 경우의 수를
4H10이라는 '중복 조합'을 이용하여 풀게끔 장려하고 있다. 하지만 우리는 알고리즘에 대해 공부하고 있기 때문에 수학 공식은 다음에 다루어 보도록 하겠다.
# 브루트포스
브루트포스의 경우에는 이 문제를 어떻게 해결할 수 있을까???
의문에 앞서 브루트포스는 말 그대로 모든경우의 수를 찾는다는 것에 초점을 맞출 필요가 있다.
즉, a = 1, b = 1, c = 1, c = 1부터 시작하여 a = 100, b = 100, c = 100, d = 100까지 총
1억개의 경우의 수를 모두 찾아보면서 a + b + c + d = 10 이 되는 값을 탐색하는 것이다.
따라서 브루트포스의 장점은 모든 경우의 수를 탐색하다보니 만족하는 값을 100% 찾아낼 수 있지만 반대로 모든 경우의 수를 판단해야하는 만큼 조합 가능한 경우의 수가 많을수록 많은 메모리 낭비가 일어난다는 단점이 존재한다.
# 백트래킹
백트래킹은 해당 노드의 유망성을 판단하는 기법이다. 즉, 해당 범위 안의 조건을 추가하여 값의 유망성을 판단하는 것이다. 만약 하나라도 a = 11이 된다면 a + b + c + d = 10 이 되지 않기 때문에 a가 11 이상일 경우에는 탐색하지 않는다. 따라서 필요한 자원을 많이 절약할 수 있다.
# DFS(깊이 우선 탐색)
DFS(깊이우선탐색)은 트리순회의 한 형태다. 하나의 순회 알고리즘으로 백트래킹에 사용하는 대표적인 탐색 알고리즘이다. 즉, 백트래킹 = DFS가 아니라 백트래킹의 방법 중 하나가 DFS인 것이다. 그 외에도 BFS(너비우선탐색) 등 다양한 방법으로 백트래킹을 구현할 수 있다.
DFS 알고리즘을 설명하자면 0 0 0 0, 0 0 0 1, 0 0 0 2, ⋯ 이런식으로 탐색하는 방법인데, 그림으로 보자면 다음과 같다.

말 그래도 깊이를 우선으로 먼저 탐색하는 방법이다.
즉, 백트래킹 문제를 DFS 방법을 통해 구현하는 것이 이번 문제의 포인트다. 좀 더 구체적인 설명은 나중에 DFS, BFS 카테고리도 있으니 이 때 설명하도록 하겠다.
그럼 이제 어떻게 구현해야하는지가 관건이다. 문제에서 N과 M이 주어지고, 중복되는 수를 제외한 모든 경우의 수를 탐색하면 된다. 그럼 기본적으로 재귀를 통해 풀어볼 수가 있겠다.
이 때 재귀를 하면서 이미 방문한 노드(값)이라면 다음 노드를 탐색하도록 하기 위해(유망한 노드인지 검사하기 위해) N 크기의 boolean 배열을 생성하고, 탐색과정에서 값을 담을 int 배열 arr 을 생성한다.
dfs 함수에는 N과 M을 변수로 받아야하는 건 당연지사, depth 변수를 추가해야한다. depth를 통해 재귀가 깊어질 때마다 depth를 1씩 증가시켜 M과 같아지면 더이상 재귀를 호출하지 않고 탐색과정 중 값을 담았던 arr 배열을 출력해주고 return 하는 역할을 위해서다.
코드로 보면 아래와 같다.
boolean[] visit = new boolean[N];
int[] arr = new int[M];
public static void dfs(int N, int M, int depth) {
if (depth == M) {
for (int val : arr) {
System.out.print(val + " ");
}
System.out.println();
return;
}
for (int i = 0; i < N; i++) {
if (visit[i] == false) {
visit[i] = true;
arr[depth] = i + 1;
dfs(N, M, depth + 1);
visit[i] = false;
}
}
return;
}
중복되는 수는 담을수 없기에 방문할 필요조차 없다. 즉, 방문 상태를 판단하기 위해 visit[] 배열이 있는 것이고, 해당 index가 방문하지 않는 노드(값)일 때만 재귀호출을 해주면 된다. 이게 백트래킹의 가장 기초라 할 수 있다.
물론 N과 M 을 함수 인자로 안넘겨도 된다. N과 M은 자체 값이 변경되거나 할 일이 없기 때문에 전역변수로 바꾸어도 무방하다. 이에 대한 것은 마지막 방법에서 설명하겠다. (자바에서는 static이라는 정적 키워드를 이용하여 전역변수처럼 활용할 수 있다. main 메소드는 static 메소드라 정적 메소드에서 외부 변수를 쓰려면 해당 변수 또한 정적 변수여야 하기 때문에 main 밖의 변수 또한 static이 붙는다. 그래서 혼용하여 쓰기 때문에 일단 이 글에서는 정적변수 = 전역변수 라고 생각하고 읽도록 하자)
# 코드 분석
import java.util.*;
public class Main{
public static int[] arr;
public static boolean[] visit;
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int m = scan.nextInt();
int n = scan.nextInt();
visit = new boolean[m];
arr = new int[n];
dfs(m,n,0);
}
public static void dfs(int m, int n, int depth){
if(depth == n){
for(int val : arr) {
System.out.print(val + " ");
}
System.out.println();
return;
}
for(int i = 0; i < m; i++){
if(!visit[i]){
visit[i] = true;
arr[depth] = i + 1;
dfs(m,n,depth + 1);
visit[i] = false;
}
}
}
}
'백준 문제 풀이' 카테고리의 다른 글
| [BOJ - JAVA] 15655 - N과 M 6 (백트래킹) (0) | 2021.09.24 |
|---|---|
| [BOJ - JAVA] 15654 - N과 M 5(백트래킹) (0) | 2021.09.24 |
| [BOJ - JAVA] 15652 - N과 M 4(백트래킹) (0) | 2021.09.24 |
| [BOJ - JAVA] 15651 - N과 M 3(백트래킹) (0) | 2021.09.24 |
| [BOJ - JAVA] 15650 - N과 M 2(백트래킹) (0) | 2021.09.24 |




