-
[BOJ - JAVA] 11722 - 가장 긴 감소하는 부분 수열 본문
728x90
반응형
# 주소
https://www.acmicpc.net/problem/11722
11722번: 가장 긴 감소하는 부분 수열
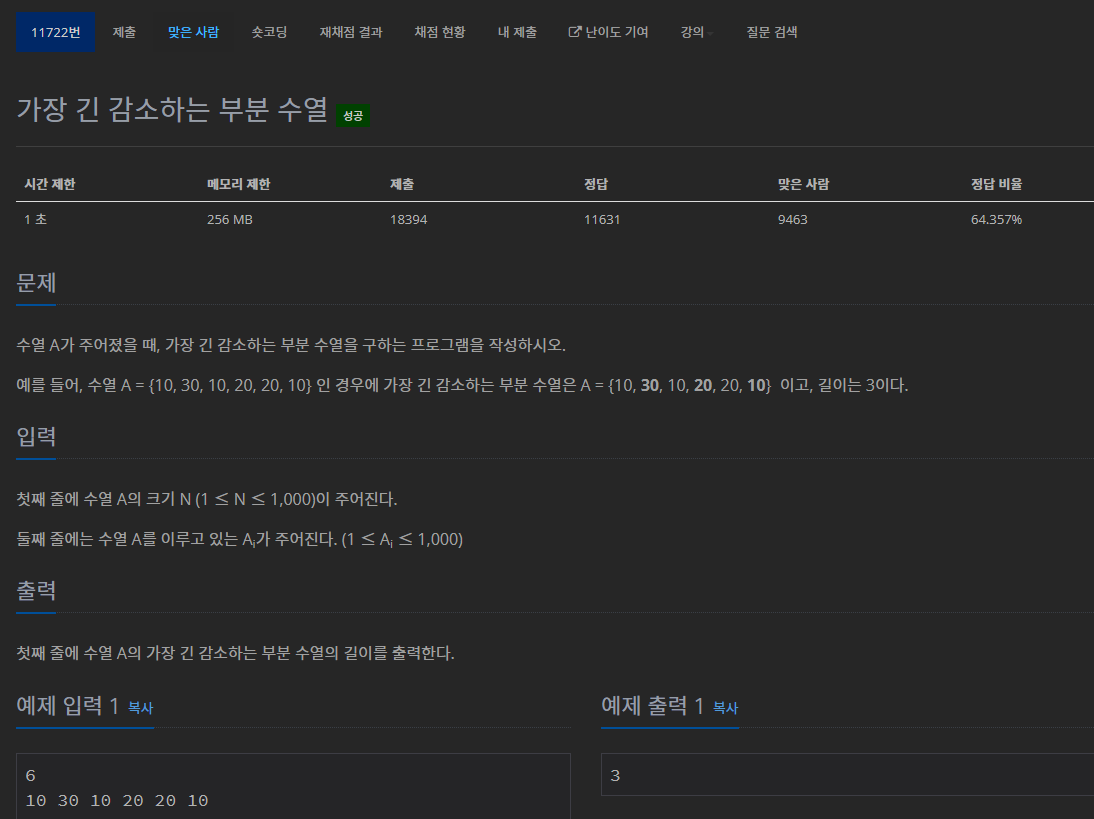
수열 A가 주어졌을 때, 가장 긴 감소하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 30, 10, 20, 20, 10} 인 경우에 가장 긴 감소하는 부분 수열은 A = {10, 30, 10, 20, 20, 10}
www.acmicpc.net
# 문제
# 문제 해설 및 코드 리뷰
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int arr[] = new int[n + 1];
int dp[] = new int[n + 1];
for (int i = 1; i <= n; i++)
arr[i] = sc.nextInt();
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = 1;
for (int j = 0; j < i; j++) {
if (arr[i] < arr[j] && dp[i] <= dp[j]) {
dp[i] = dp[j] + 1;
} else if (arr[i] == arr[j]) {
dp[i] = dp[j];
}
}
}
int max = 0;
for (int i = 1; i <= n; i++)
max = Math.max(dp[i], max);
System.out.println(max);
sc.close();
}
}
정말 단순합니다. 단순해서 Scanner로 풀고 이클립스에 자꾸 경고가 떠서 마지막엔 sc.close()를 하여 scan도 닫아주었습니다.
핵심 코드 내용을 살펴보자면, 이 문제도 LIS처럼 이중 for문을 이용하여 풀었습니다.
문제 유형은 DP에 가깝지만 DP 중에서도 가장 쉬운 유형이 아닐까 싶습니다.
arr[i] < arr[j]에 대해서, dp의 값을 +1씩 더해주었습니다.
예를 살펴보겠습니다.
| 예 | 10 | 20 | 9 | 8 |
| arr[i] | 10 | 20 | 9 | 8 |
| dp[i] | 1 | 1 | 2 | 3 |
dp[i]와 dp[j](j는 i보다 작음) 값이 같으면 dp의 값을 그대로 유지합니다.
그래서 dp[i]의 마지막 값은 3이 되겠습니다.
어려운 부분은 없을것이라 생각합니다.
DP의 개념이 이해가 안된다면 펜으로 써가면서 하거나 표를 그려서 해보시면 금방 이해되실 거라 생각합니다.
감사합니다.
728x90
반응형
'백준 문제 풀이' 카테고리의 다른 글
| [BOJ - JAVA] 17427 - 약수의 합2 (0) | 2021.10.01 |
|---|---|
| [BOJ - JAVA] 1037 - 약수 (0) | 2021.09.30 |
| [BOJ - JAVA] 11055 - 가장 큰 증가 부분 수열 (0) | 2021.09.30 |
| [BOJ - JAVA] 1339 - 단어 수학(그리디, 브루트포스) (0) | 2021.09.30 |
| [BOJ - JAVA] 10974 - 모든 순열 (0) | 2021.09.28 |
Comments




