-
[BOJ - JAVA] 1912 - 연속합(DP) 본문
# 주소
https://www.acmicpc.net/problem/1912
1912번: 연속합
첫째 줄에 정수 n(1 ≤ n ≤ 100,000)이 주어지고 둘째 줄에는 n개의 정수로 이루어진 수열이 주어진다. 수는 -1,000보다 크거나 같고, 1,000보다 작거나 같은 정수이다.
www.acmicpc.net
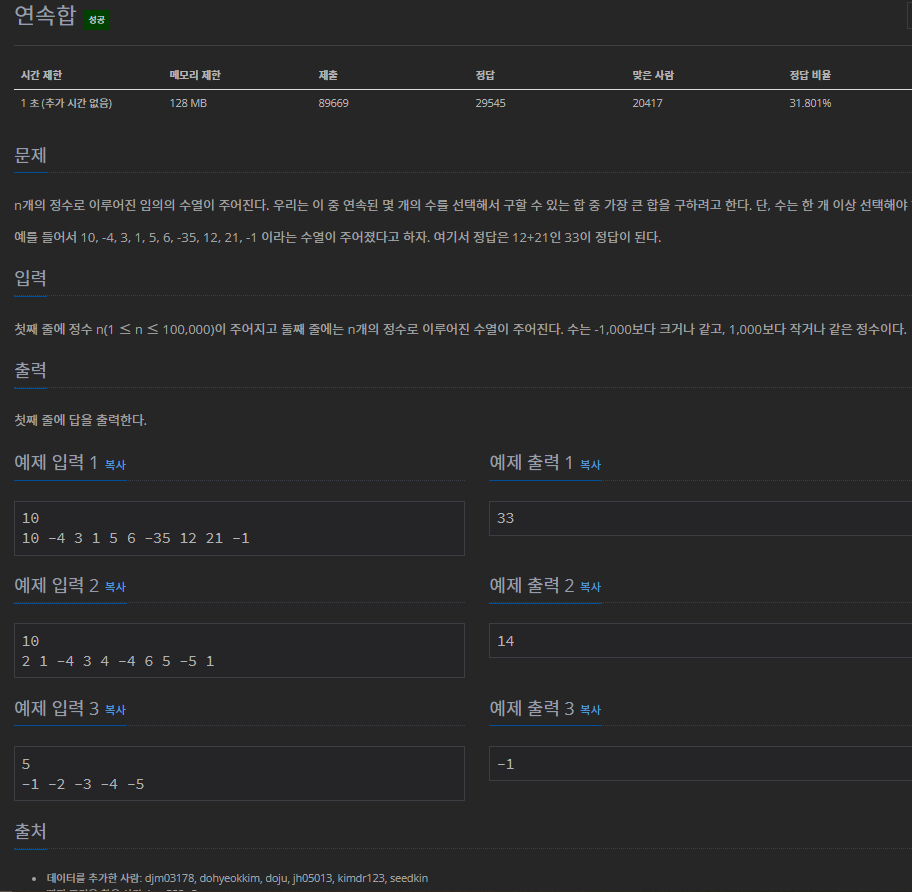
# 문제
# 문제 해설 및 코드 리뷰 (처음 작성한 코드)
import java.util.*;
public class Main{
public static void main(String[] args){
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int[] arr = new int[n];
int[] dp = new int[n];
for(int i = 0; i < n; i++){
arr[i] = scan.nextInt();
}
dp[0] = arr[0];
ArrayList<Integer> list = new ArrayList<>();
for(int i = 1; i < n; i++){
if(arr[i] >= 0){
dp[i] += arr[i];
}
if(arr[i] < 0){
list.add(dp[i-1]);
}
}
Collections.sort(list);
System.out.println(list.get(list.size() - 1));
}
}처음엔 음수의 상황은 고려하지 않고 연속합을 구했습니다.
그렇기 때문에 양수의 값들은 계속 더하고 음수 값이 등장할 때마다 list에 담았습니다.
그런데 문제의 예제들로는 이클립스에서 잘 작동했지만 음수의 값이 작고 주변 양수의 값이 있을 경우에는 최대값이 더 커질 수 있다는 사실을 간과했습니다. 따라서 새로 로직을 짜야만 했습니다. 그것이 밑의 코드입니다.
# 새로 작성한 코드
import java.util.*;
public class Main{
public static int[] arr;
public static Integer[] dp;
public static int max;
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
arr = new int[n];
dp = new Integer[n];
for(int i = 0; i < n; i++)
arr[i] = scan.nextInt();
dp[0] = arr[0];
max = arr[0];
sum(n-1);
System.out.println(max);
}
public static int sum(int n) {
if(dp[n] == null) {
dp[n] = Math.max(sum(n-1) + arr[n], arr[n]);
max = Math.max(dp[n], max);
}
return dp[n];
}
}
일단 int와 Integer의 차이를 이해할 필요가 있습니다.
1) int - Primitive 자료형(long, float, double, char 등등)
실제 값을 저장할 때 우리가 항상 사용해오던 int타입입니다. 산술 연산에 능하지만 null로 초기화가 불가능하고 0으로 초기화 할 수 있습니다.
2) Integer - Wrapper 클래스(객체)
실제 값을 가리키는 주소값을 저장합니다. 클래스 타입이므로 Unboxing을 하지 않으면 산술 연산이 불가능하지만 null값을 처리하는데 용합니다. 따라서 SQL과 연동할 경우 자주 사용됩니다. 직접적인 산술연산은 불가능하므로 기본형을 제외한 모든 타입은 Reference Type이며 java.lang.Object를 상속합니다.
(근데 dp를 int타입으로 두고 dp[n] == 0일 때로 풀이하셔도 정답에는 지장이 없습니다!! 실행 속도를 조금 더 빠르게 하기 위해 값을 가져오는 것이 아닌, 참조 주소를 가져와서 연산하는 것이 훨씬 더 빠르기 때문에 (C의 포인터랑 비슷함) 이 방법을 차용했습니다. 저도 두고두고 써먹기 위해서이기도 하고 이 방법을 메모이제이션이라는 용어로 기억하시면 좋을 것 같습니다.)
이제 본격적으로 문제를 해설하겠습니다.
이 문제는 재귀함수로 푸는 것이 용이합니다. 처음엔 백트래킹으로 풀려고 했으나 제한 시간이 1초인 점을 고려하여, 또 입력값이 10만이 맥시멈인걸 고려하여 점화식과 재귀로 푸는것이 좋습니다.
가장 중요한 부분은
public static int sum(int n) {
if(dp[n] == null) {
dp[n] = Math.max(sum(n-1) + arr[n], arr[n]);
max = Math.max(dp[n], max);
}
return dp[n];
}여기 부분입니다. 단 3줄의 코딩으로 sum의 최대값을 구할 수 있습니다.
dp[n]은 sum(n-1) + arr[n] 과 arr[n]중 더 큰 값을 dp[n]에 담는다는 내용입니다.
그러니까 sum(n-1)일 때 n-1까지의 인덱스 이하의 sum 중 최대값이 존재할텐데요.
n-1까지의 인덱스의 sum에 arr를 더한 것과 그냥 arr 중 더 큰 값을 dp에 저장합니다. 그렇게 되면 dp는 음수가 들어온다 하더라도 다음 값도 더할 수 있습니다.
예를 들어 3 4 -4 6 5 의 경우, dp[2] = 7입니다( i = 1,2,3,4,5).
그리고 dp[3] = 3이고 dp[4] = 9, dp[5] = 14입니다.
제 아무리 음수가 들어온더 하더라도 음수를 더했을 때 값이 음수의 값보다 크다고 한다면 그대로 연속합을 구할 수 있는 것입니다.
감사합니다.
'백준 문제 풀이' 카테고리의 다른 글
| [BOJ - JAVA] 1010 - 다리 놓기(DP, 조합) (0) | 2021.10.20 |
|---|---|
| [BOJ - JAVA] 2579 - 계단 오르기(DP, 점화식) (0) | 2021.10.20 |
| [BOJ - JAVA] 1895 - 필터(슬라이딩 윈도우) (0) | 2021.10.18 |
| [BOJ - JAVA] 10870 - 피보나치 수열 5(DP) (0) | 2021.10.17 |
| [BOJ - JAVA] 1365 - 꼬인 전깃줄(이분탐색, 가장 긴 증가하는 부분수열) (0) | 2021.10.15 |




